10814. Система неперескающихся множеств 2

Реализуйте систему непересекающихся множеств. На структуре данных нужно выполнить набор запросов двух типов:

· union u v – объединить два множества, содержащие u и v соответственно;

· get v – найти множество, которому принадлежит v, найти минимальный и максимальный элемент, а также число элементов в множестве.

Вход. Первая строка содержит два числа n и m (1 ≤ n, m ≤ 3 * 10⁵) – число элементов и число запросов. Далее идут m строк запросов, по одному на строке.

Для запросов union строка выглядит как union u v (1 ≤ u, v ≤ n).

Для запросов get строка выглядит как get v (1 ≤ v ≤ n).

Выход. Выведите результат каждой операции get по одной на строке в соответствующем порядке. Каждый результат состоит из трёх чисел: минимальный элемент, максимальный элемент и число элементов.

Пример входа	Пример выхода
5 11 union 1 2 get 3 get 2 union 2 3 get 2 union 1 3 get 5 union 4 5 get 5 union 4 1 get 5	3 3 1 1 2 2 1 3 3 5 5 1 4 5 2 1 5 5

РЕШЕНИЕ

система непересекающихся множеств

Анализ алгоритма

Реализуем систему непересекающихся множеств с эвристиками.

В операции union поддерживаем пересчет минимального и максимального элементов множества, а также количество его элементов.

Изначально имеем n множеств из одного элемента, причем i-ое множество содержит только число i. Минимум amin[i] и максимум amax[i] в i-ом множестве изначально равен i. Размер i-го множества cnt[i] равен 1.

Пусть множество с представителем y добавляется во множество с представителем x.

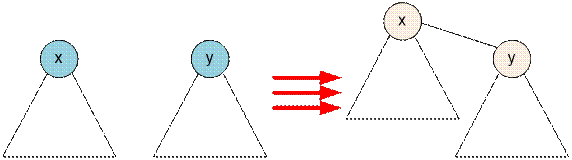
Тогда минимум, максимум и количество элементов во множестве пересчитывается следующим образом:

· cnt[x] = cnt[x] + cnt[y];

· amin[x] = min(amin[x], amin[y]);

· amax[x] = max(amax[x], amax[y]);

Пример

Промоделируем запросы из примера.

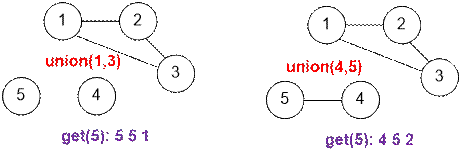
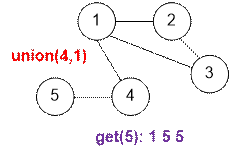
Реализация алгоритма

Объявим рабочие массивы:

· parent – массив предков;

· depth – содержит высоту дерева, используется для эвристики;

· amin, amax – массивы поддерживают минимальный и максимальный элементы в множествах;

· cnt – массив для поддержки количества элементов в множествах;

#define MAX 300001

int parent[MAX], depth[MAX], amin[MAX], amax[MAX], cnt[MAX];

Функция Repr возвращает представителя множества, в котором находится v.

int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

Функция Union объединяет множества с элементами x и y.

void Union(int x, int y)

{

Находим представителей x и y.

x = Repr(x), y = Repr(y);

if (x == y) return;

Эвристика по высоте деревьев. Множество с меньшей высотой присоединяем к множеству с большей высотой.

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

Количество вершин из множества с элементом y прибавляем во множество где находится x.

cnt[x] += cnt[y];

Пересчитываем минимальный и максимальный элементы в множествах.

if (amin[y] < amin[x]) amin[x] = amin[y];

if (amax[y] > amax[x]) amax[x] = amax[y];

}

Основная часть программы. Читаем входные данные. Инициализируем массивы. Изначально имеем n множеств из одного элемента. Минимум и максимум в i-ом множестве равен i. Размер i-го множества cnt[i] равен 1.

Высота каждого множества depth[i] изначально считается равной 0.

scanf("%d %d", &n, &m);

for (i = 1; i <= n; i++) parent[i] = i;

for (i = 1; i <= n; i++) amin[i] = amax[i] = i;

for (i = 1; i <= n; i++) cnt[i] = 1;

Последовательно обрабатываем m запросов.

for (i = 0; i < m; i++)

{

scanf("\n");

scanf("%s %d", s, &u);

if (s[0] == 'u')

{

scanf("%d", &v);

Объединяем множества содержащие элементы u и v.

Union(u, v);

}

else

{

Находим представителя множества, содержащего элемент u.

int u1 = Repr(u);

Выводим минимальный и максимальный элемент множества, а также количество его элементов.

printf("%d %d %d\n", amin[u1], amax[u1], cnt[u1]);

}

}